1. INTRODUCTION

Multivariate linear regression analysis of meteorological data from the Utah Mesonet (Stiff, 1997) has been tested as a tool for both data quality assessment and as a method for objectively analyzing data in complex terrain. A least-squares fit to the pressure, temperature and dew point data across the Mesonet domain is accomplished by assuming a linear variance of the surface data (e.g. temperature) in x, y, and z space. The linear regression analysis provides a tool for a) assessing the quality of data and b) objectively analyzing surface meteorological data (e.g. as input into atmospheric models) in the mountainous terrain of the Utah Mesonet.

Objective schemes commonly used in meteorological analysis (e.g., Barnes, 1964) use a weighting of values of nearby data to determine an estimate at a given location. Many of these schemes are used for analysis of meteorological variables on quasi-horizontal surfaces in which weights are dependent on the horizontal distance an observation is from an analysis point. In complex terrain a two dimensional smoothing of observations (with typical station densities) will produce unreliable estimates given the strong dependency of the meteorological variables on the vertical dimension. Use of three dimensional weighting schemes are possible with these schemes, but are not necessarily straight forward in application. The multivariate linear regression analysis was tested as a method for use in complex terrain since the use of the three spatial dimensions is consistent and simple.

2. REGRESSION ANALYSIS

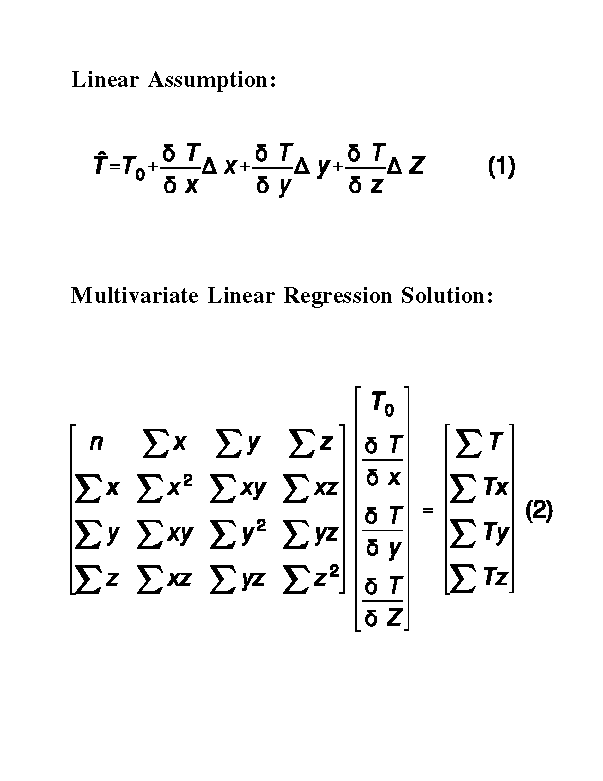
The key to use of the regression analysis is the assumption that a linear fit of the meteorological variable in three dimensions will be a relatively good fit over the domain chosen. Using temperature as an example, the linear fit desired would be described as:

where T is the temperature estimate for a given location (in three dimensional space) given the temperature at the origin and the temperature gradients (which are generated from the regression analysis).

Determination of T0 and the spatial derivatives of T are obtained from multivariate linear regression (e.g., Strait, 1983), using observational data at a single time period. Extension of this problem to the time dimension was not anticipated to improve results due to nonlinearities in time. The solution of the standard two variable linear regression can be extended to this multi-dimensional problem. The matrix of equations that needs to be solved are referred to as the normal equations (2). Where n is the number of stations reporting temperature. x ,y, and z are the positional coordinates. Standard matrix inversion techniques can be used to solve (2) for the temperature at the origin and the temperature gradients.

3. APPLICATION TO MESONET DATA

The linear regression fit to the Utah Mesonet data is estimated every 15 minutes using the latest data available from the approximately 300 Mesonet stations (within an hour period). The Mesonet is a collection of data from several instrument networks in the intermountain West and each network has different reporting frequencies ranging from hourly to 5 minutes intervals. Using data from within the past hour allows for a more significant number of data points to be used in the regression analysis and provides for more stable estimates over time. Figure 1 depicts the time series of the temperature estimate from the regression analysis as well as the observed data at Salt Lake City (1286 m ASL) on September 4, 1997, while Figure 2 depicts the same for UT3 (Parleys Summit, 2316 m ASL). Greater noise in the regression estimate during the first half hour are attributed to a lower number of stations being available for the analysis.

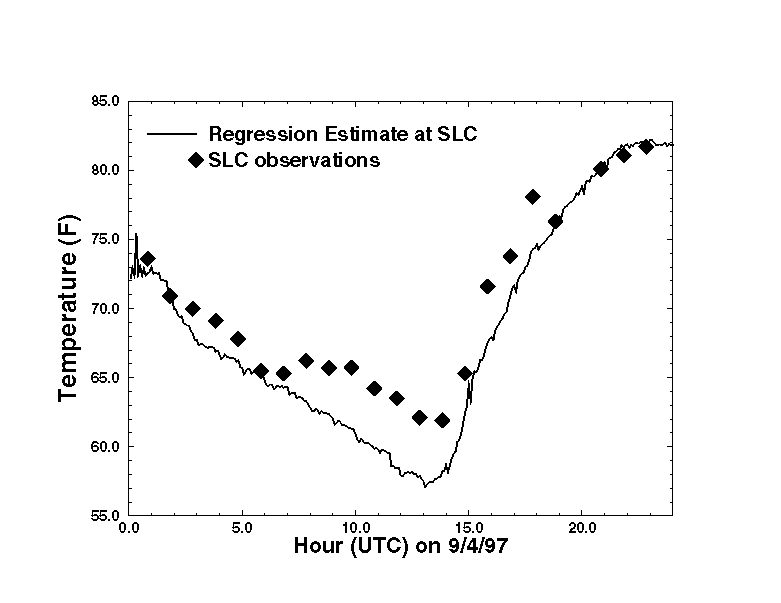
Figure 1: A comparison of the linear regression esimates of temperature at Salt Lake City, UT to the observed data.

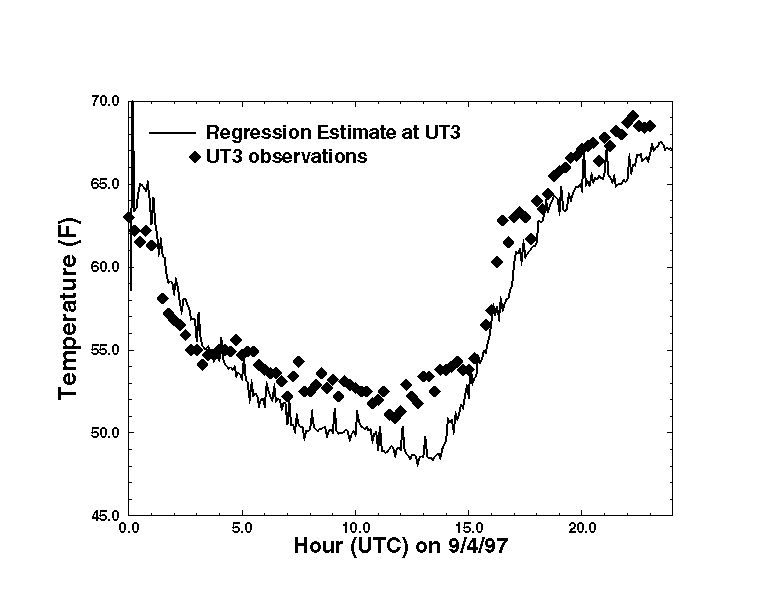
Figure 2: A comparison of the linear regression esimates of temperature at Parleys Summit (UT3) to the observed data.

4. USE IN DATA QUALITY ASSURANCE

The multivariate analysis provides a method to obtain objective values of a meteorological quantity at a station location to compare to the actual data values. The individual station value will have less of a weight in determination of the objective estimate (at that location) in comparison to other objective analysis approaches. It is important that the regression provide a reasonably close approximation to the observational data in order for evaluation of data quality to be reliable. Figure 3 depicts the agreement to which the regression estimates compare to the station data. The differences shown are daily average differences between the regression estimates and the actual values at each station location. Note that the clear majority of stations agree to within +/- 5 degrees F. Outliers of significance are observable and are believed to be questionable data. The quality of this comparison gives confidence that the regression is providing estimates that can provide utility in data quality assurance for the Mesonet. Similar results can also be shown from the pressure and dew point observations.

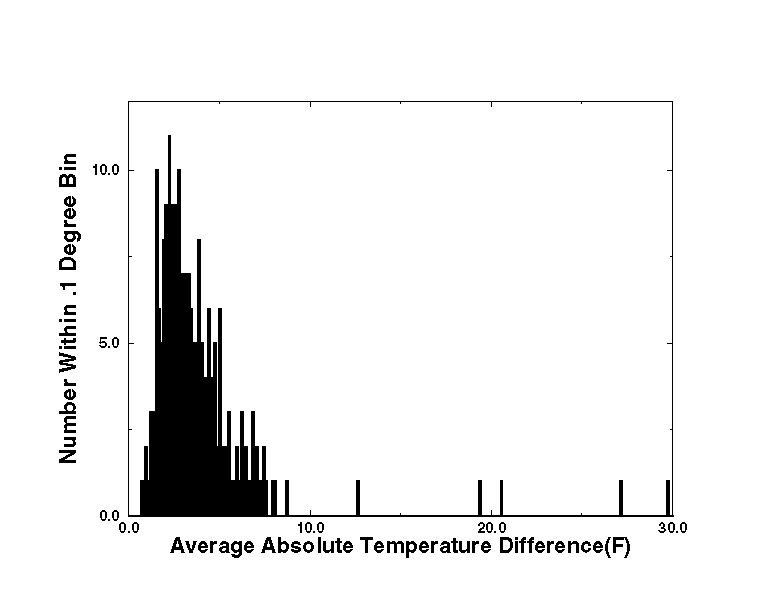
Figure 3: The difference between the regression and observations (daily average) shows most stations agree to within several degrees.

The quality of the regression fit allows for the use of the regression analyses in real-time data flagging. Data quality flags are currently being generated for data in the Utah Mesonet in a real-time fashion based on agreement between the regression and the actual data over the past 6 hourly period. For example, if the temperature data at station X is different from the regression (on average) over the last 6 hours by over 10 degrees F, the current data point is flagged. Data currently being flagged by such a technique includes the temperature, pressure and dewpoint data. It was not thought to be useful to use this technique to flag data departing from the regression at shorter time intervals since they might be caused by valid meteorological phenomenon.

The linear fit can be used to provide objective estimates of data at the Mesonet station locations for data quality verification. Erroneous observations are shown to be detectable, as well as data base errors such as misspecification of station altitude, by comparison of the actual data to the linear fit. While the linear fit can not be expected to account for small-scale events within the Mesonet domain, data comparisons over longer periods of time are useful.

5. USE IN OBJECTIVE ANALYSIS

The linear regression analysis also provides a tool for objectively analyzing surface meteorological data (e.g., as input into atmospheric models) in the mountainous terrain of the Utah Mesonet. The regression fit, especially the vertical gradient, is helpful in providing estimates in data poor regions. Figure 4 depicts a regression based analysis of the surface temperature across northwest Utah on September 4, 1997. The analysis is dominated by the topography, which is shown in Figure 5.

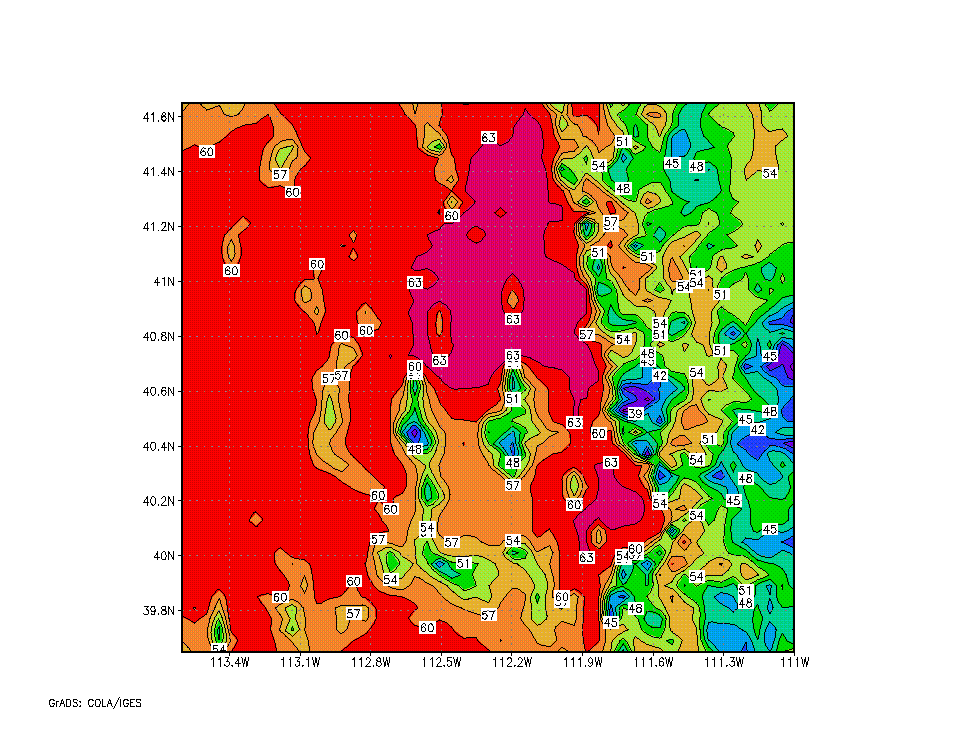
Figure 4: A regression based objective analysis of temperature across northwest Utah (2 degrees F contours).

Figure 5: Elevation (ASL) in meters across northwest Utah (200m contour interval).

The linear fit of the regression analysis can be improved upon in data rich areas by the additional use of a Barnes' objective analysis of the differences between the regression fit and the actual data. The Barnes' analysis weighting functions can be selected as such (i.e. by selection of the smoothing scale radius) to add information back into the analysis where station data is available and to fall back closer to the regression fit in data poor regions. Figure 6 is an example of the Barnes' analysis smoothed difference field between the regression and actual temperatures over northwest Utah during extreme meteorological conditions on January 13, 1997. Real-time displays of this type of temperature analysis over the Wasatch Front area of Utah are created hourly.

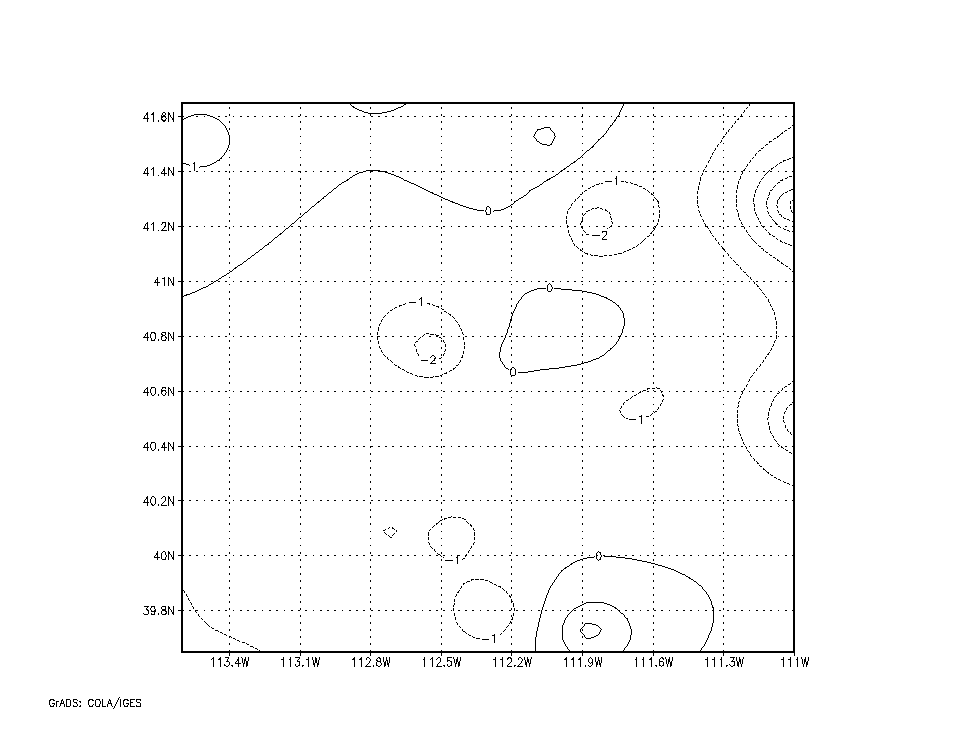
Figure 6: Temperature difference between regression and observations smoothed with Barnes' analysis.

6. CONCLUDING COMMENTS

Multivariate linear regression analysis of meteorological data has been shown to be a useful tool for objective analysis of surface data in complex terrain. This analysis scheme can be used in the context of quality assurance activities or as a part of an objective analysis algorithm for specifying surface conditions for use in forecasting or numerical weather prediction.

The regression analysis has been used to flag data from the Utah Mesonet using analysis of pressure, temperature and dew point. The analysis can be done quickly and has allowed for flagging of data in real time. Application to other meteorological variables has not been fully investigated, though not expected to produce as high quality results. For example, the surface wind field in the mountainous regions are much more complex than the temperature field.

The regression analysis has been shown to provide useful surface analyses. The Barnes' analysis of the difference between the regression estimates and the actual data can be used to introduce nonlinear variations (e.g. mesoscale features such as fronts), though confidence in the observations should be high to conduct such an analysis. Comparison of regression analysis estimates to more complicated data assimilation systems (e.g. Brewster, 1996) are anticipated in the near future over portions of the Utah Mesonet area.

7. REFERENCES

Barnes, S.L., 1964: A technique for maximizing details in numerical weather map analysis. J. Appl. Meteor., 3, 396-409.

Stiff, C.J., 1997: The Utah Mesonet. Master's thesis, University of Utah.

Strait, P.T., 1983: A first course in probability and statistics with applications, Harcourt Brace Jovanovich, 581 pp.

Brewster, K., 1996: Implementation of a Bratseth analysis scheme including Doppler radar. Preprints, 15th Conf. and Forecasting, AMS Boston, 92-95.